redo log
在 MySQL 中,如果每一次的更新操作都需要写进磁盘,然后磁盘也要找到对应的那条记录,然后再更新,整个过程 IO 成本、查找成本都很高。为了解决这个问题,MySQL 的设计者就采用了日志(redo log)来提升更新效率。
而日志和磁盘配合的整个过程,其实就是 MySQL 里的 WAL 技术,WAL 的全称是 Write-Ahead Logging,它的关键点就是先写日志,再写磁盘。
具体来说,当有一条记录需要更新的时候,InnoDB 引擎就会先把记录写到 redo log(redolog buffer)里面,并更新内存(buffer pool),这个时候更新就算完成了。同时,InnoDB 引擎会在适当的时候(如系统空闲时),将这个操作记录更新到磁盘里面(刷脏页)。
redo log 是 InnoDB 存储引擎层的日志,又称重做日志文件,redo log 是循环写的,redo log 不是记录数据页更新之后的状态,而是记录这个页做了什么改动。
redo log 是固定大小的,比如可以配置为一组 4 个文件,每个文件的大小是 1GB,那么日志总共就可以记录 4GB 的操作。从头开始写,写到末尾就又回到开头循环写,如下图所示。
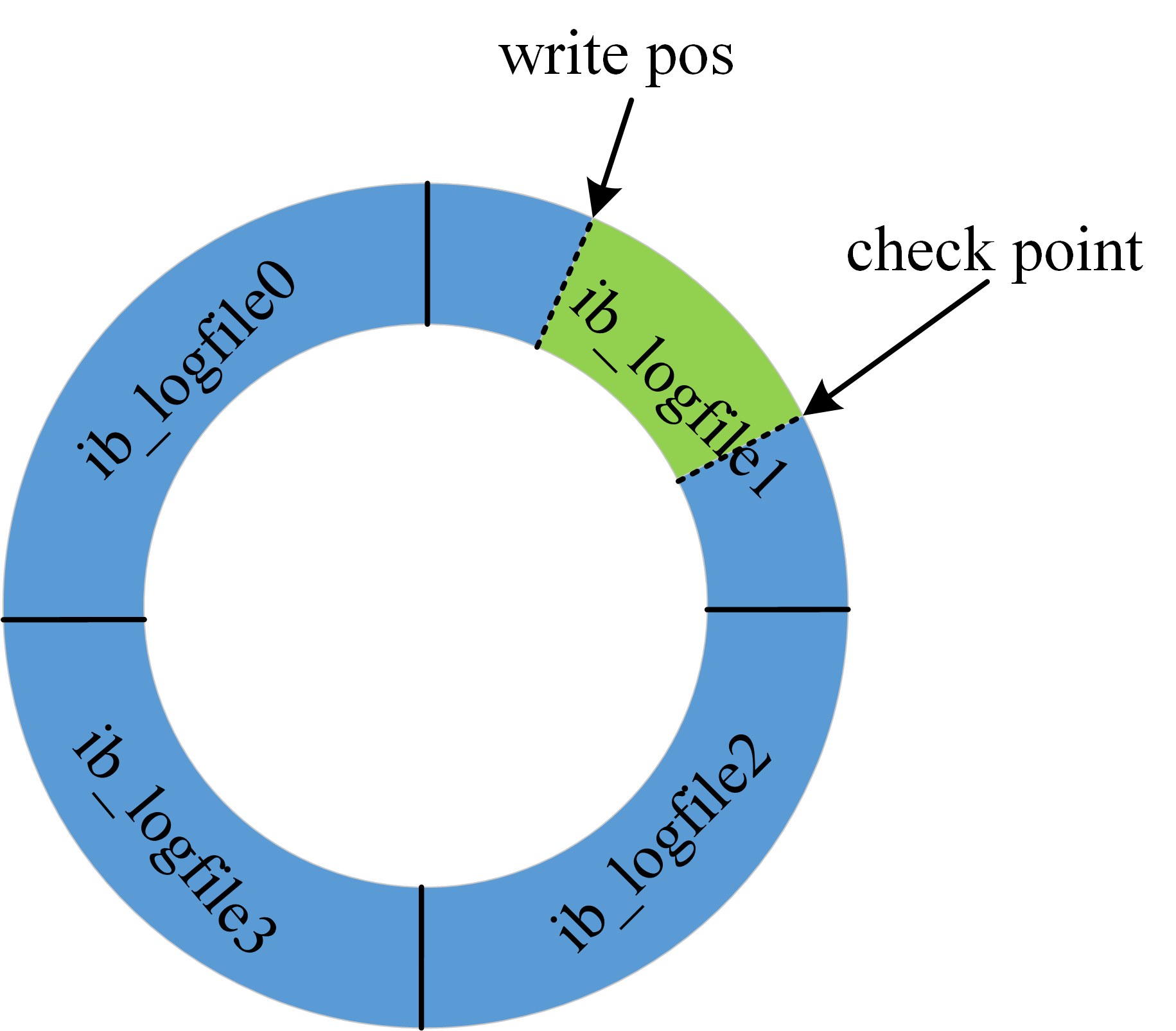
图中展示了一组 4 个文件的 redo log 日志,checkpoint 是当前要擦除的位置,擦除记录前需要先把对应的数据落盘(更新内存页,等待刷脏页)。write pos 到 checkpoint 之间的部分可以用来记录新的操作,如果 write pos 和 checkpoint 相遇,说明 redolog 已满,这个时候数据库停止进行数据库更新语句的执行,转而进行 redo log 日志同步到磁盘中。checkpoint 到 write pos 之间的部分等待落盘(先更新内存页,然后等待刷脏页)。
有了 redo log 日志,那么在数据库进行异常重启的时候,可以根据 redo log 日志进行恢复,也就达到了 crash-safe。
redo log 用于保证 crash-safe 能力。innodb_flush_log_at_trx_commit 这个参数设置成 1 的时候,表示每次事务的 redo log 都直接持久化到磁盘。这个参数建议设置成 1,这样可以保证 MySQL 异常重启之后数据不丢失。
binlog
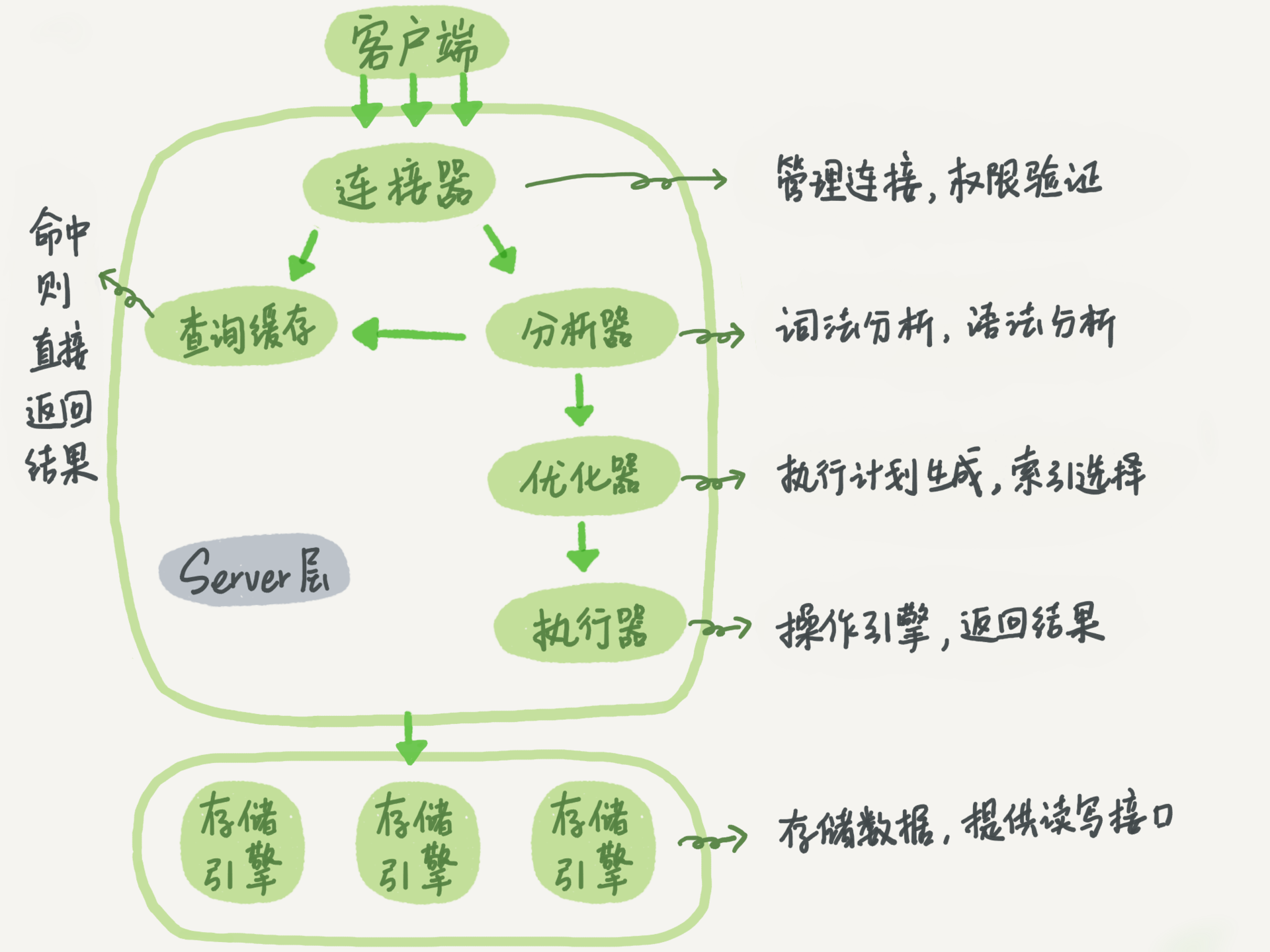
MySQL 整体来看,其实就有两块:一块是 Server 层,它主要做的是 MySQL 功能层面的事情;还有一块是引擎层,负责存储相关的具体事宜。redo log 是 InnoDB 引擎特有的日志,而 Server 层也有自己的日志,称为 binlog(归档日志)。
binlog 属于逻辑日志,是以二进制的形式记录的是这个语句的原始逻辑,依靠 binlog 是没有 crash-safe 能力的。
binlog 有两种模式,statement 格式的话是记 sql 语句,row 格式会记录行的内容,记两条,更新前和更新后都有。
sync_binlog 这个参数设置成 1 的时候,表示每次事务的 binlog 都持久化到磁盘。这个参数也建议设置成 1,这样可以保证 MySQL 异常重启之后 binlog 不丢失。
为什么会有两份日志呢?
因为最开始 MySQL 里并没有 InnoDB 引擎。MySQL 自带的引擎是 MyISAM,但是 MyISAM 没有 crash-safe 的能力,binlog 日志只能用于归档。而 InnoDB 是另一个公司以插件形式引入 MySQL 的,既然只依靠 binlog 是没有 crash-safe 能力的,所以 InnoDB 使用另外一套日志系统——也就是 redo log 来实现 crash-safe 能力。
redo log VS binlog
- redo log 是 InnoDB 引擎特有的;binlog 是 MySQL 的 Server 层实现的,所有引擎都可以使用。
- redo log 是物理日志,记录的是在某个数据页上做了什么修改;binlog 是逻辑日志,记录的是这个语句的原始逻辑。
- redo log 是循环写的,空间固定会用完;binlog 是可以追加写入的。追加写是指 binlog 文件写到一定大小后会切换到下一个,并不会覆盖以前的日志。
update 流程
有了对 redo log 和 binlog 这两个日志的概念性理解后,再来看执行器和 InnoDB 引擎在执行这个 update 语句时的内部流程。
- 执行器先找引擎取 ID=2 这一行。ID 是主键,引擎直接用树搜索找到这一行。如果 ID=2 这一行所在的数据页本来就在内存中,就直接返回给执行器;否则,需要先从磁盘读入内存,然后再返回。
- 执行器拿到引擎给的行数据,把这个值加上 1,比如原来是 N,现在就是 N+1,得到新的一行数据,再调用引擎接口写入这行新数据。
- 引擎将这行新数据更新到内存(InnoDB Buffer Pool)中,同时将这个更新操作记录到 redo log 里面,此时 redo log 处于 prepare 状态。然后告知执行器执行完成了,随时可以提交事务。
- 执行器生成这个操作的 binlog,并把 binlog 写入磁盘。
- 执行器调用引擎的提交事务接口,引擎把刚刚写入的 redo log 改成提交(commit)状态,更新完成。
下图为 update 语句的执行流程图,图中灰色框表示是在 InnoDB 内部执行的,绿色框表示是在执行器中执行的。
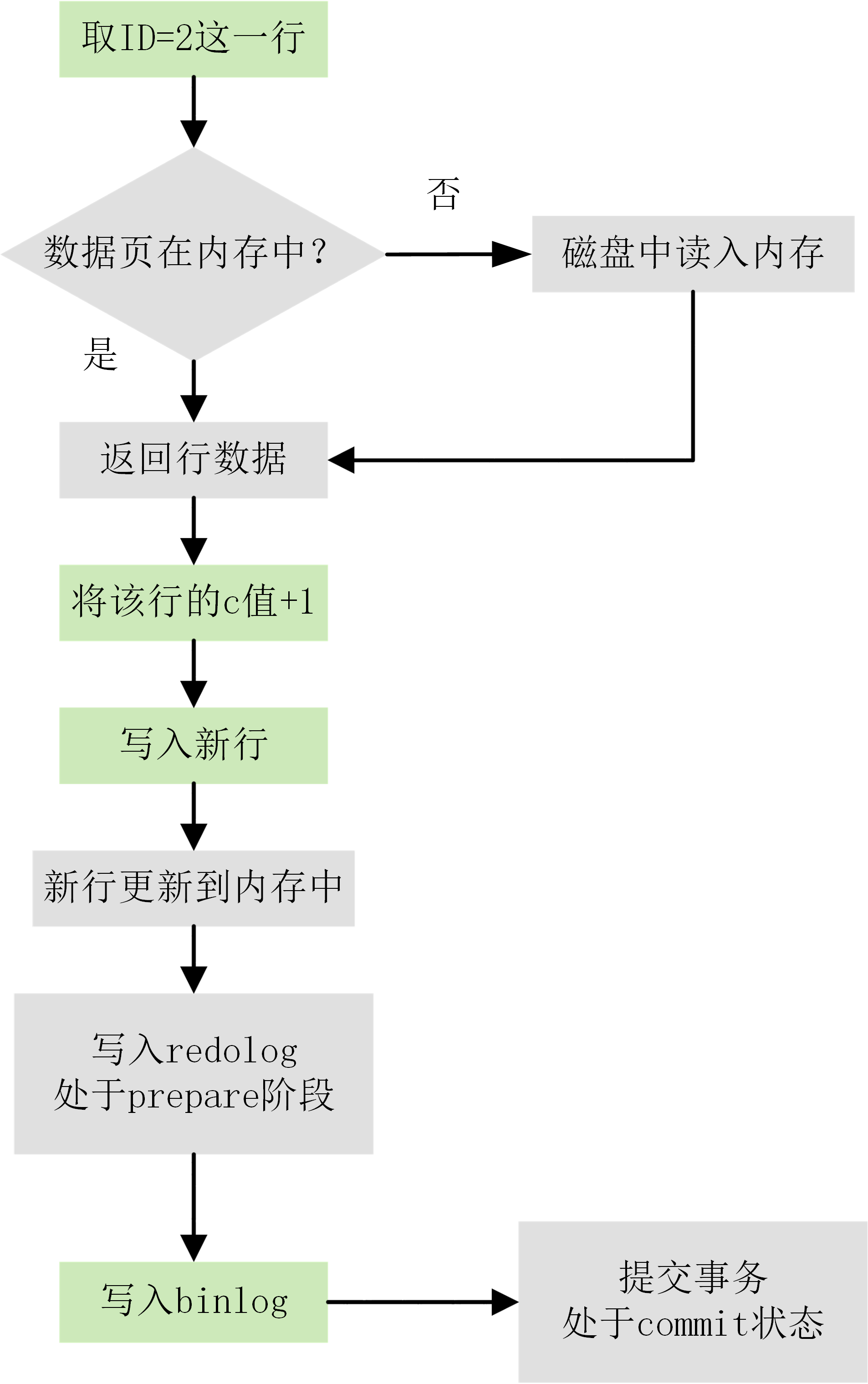
其中将 redo log 的写入拆成了两个步骤:prepare 和 commit,这就是两阶段提交(2PC)。
两阶段提交(2PC)
MySQL 使用两阶段提交主要解决 binlog 和 redo log 的数据一致性的问题。
redo log 和 binlog 都可以用于表示事务的提交状态,而两阶段提交就是让这两个状态保持逻辑上的一致。下图为 MySQL 二阶段提交简图:
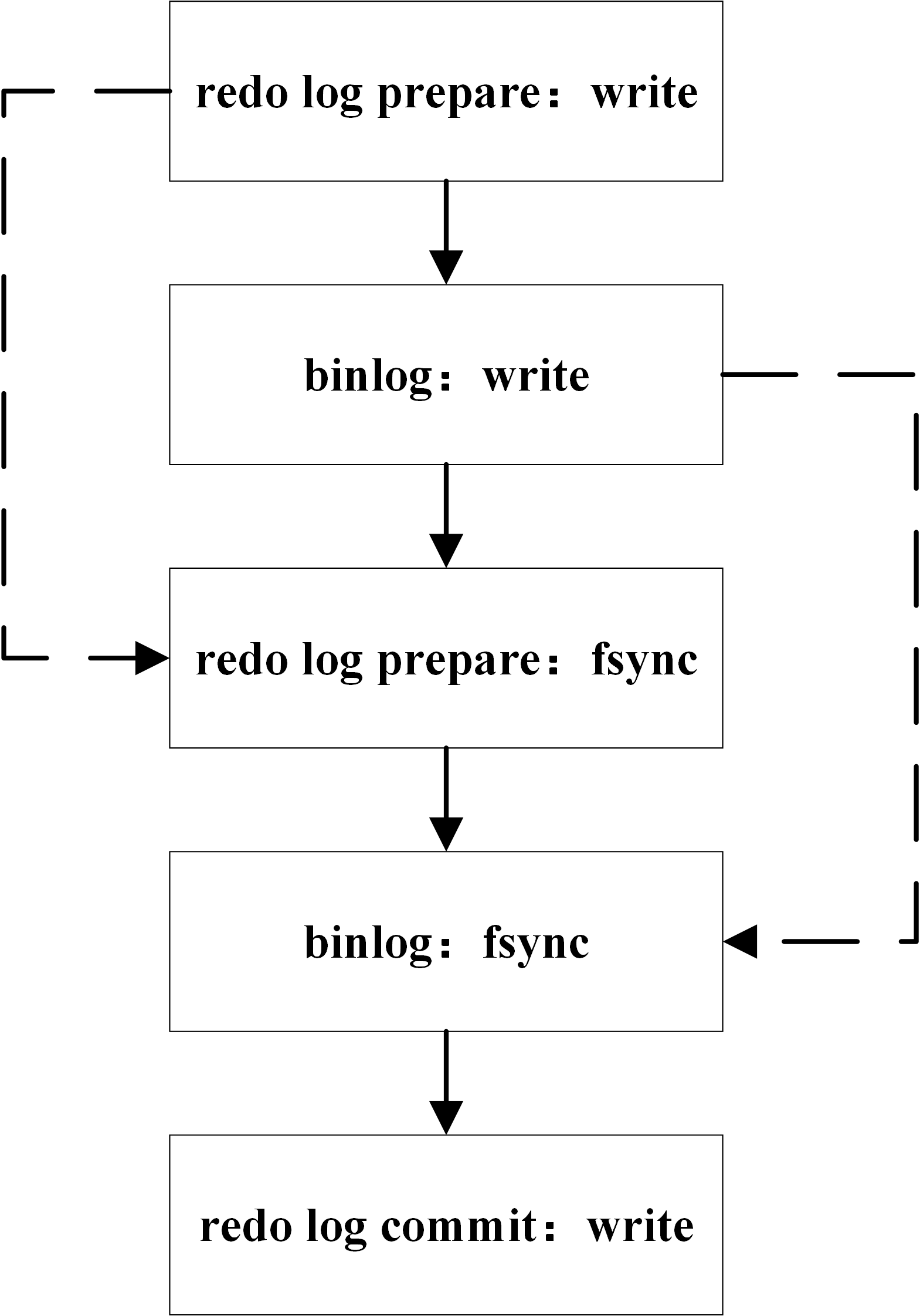
两阶段提交原理描述:
- InnoDB redo log 写盘,InnoDB 事务进入 prepare 状态。
- 如果前面 prepare 成功,binlog 写盘,那么再继续将事务日志持久化到 binlog,如果持久化成功,那么 InnoDB 事务则进入 commit 状态(在 redo log 里面写一个 commit 记录)
备注: 每个事务 binlog 的末尾,会记录一个 XID event,标志着事务是否提交成功,也就是说,recovery 过程中,binlog 最后一个 XID event 之后的内容都应该被 purge。