概念
- 图(有向图、无向图、带权图)
- 顶点
- 边
- 度(入度、出度)
存储
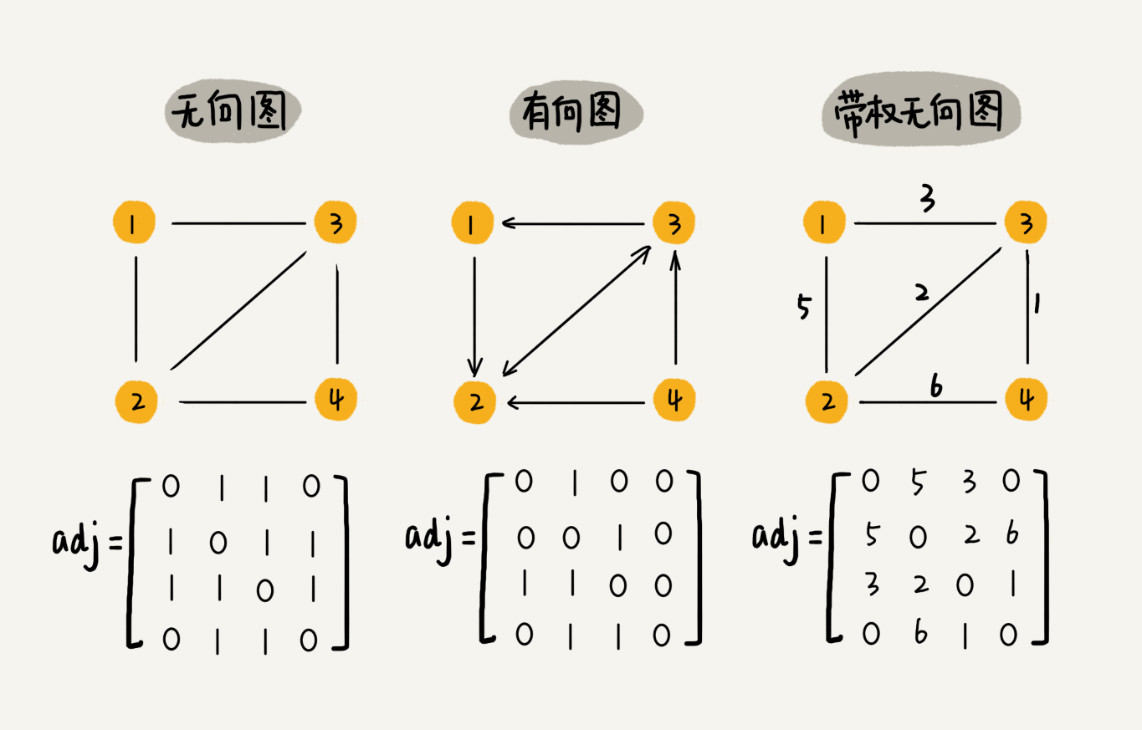
邻接矩阵
邻接矩阵的底层依赖一个二维数组。
对于无向图来说,如果顶点i与顶点j之间有边,我们就将A[i][j]和A[j][i]标记为1。
对于有向图来说,如果顶点i到顶点j之间,有一条箭头从顶点i指向顶点j的边,那我们就将A[i][j] 标记为 1。同理,如果有一条箭头从顶点 j 指向顶点 i 的边,我们就将 A[j][i] 标记为 1。
对于带权图,数组中就存储相应的权重。
优缺点
优点
邻接矩阵的存储方式简单、直接,因为基于数组,所以在获取两个顶点的关系时,就非常高效。其次,用邻接矩阵存储图的另外一个好处是方便计算。
缺点
对于无向图来说,如果我们将其用对角线划分为上下两部分,那我们只需要利用上面或者下面这样一半的空间就足够了,另外一半白白浪费掉了。
如果我们存储的是稀疏图(Sparse Matrix),也就是说,顶点很多,但每个顶点的边并不多,那邻接矩阵的存储方法就更加浪费空间了。
邻接表存储
每个顶点对应一条链表,链表中存储的是与这个顶点相连接的其他顶点。
如下图:是一个有向图的邻接表存储方式,每个顶点对应的链表里面,存储的是指向的顶点。
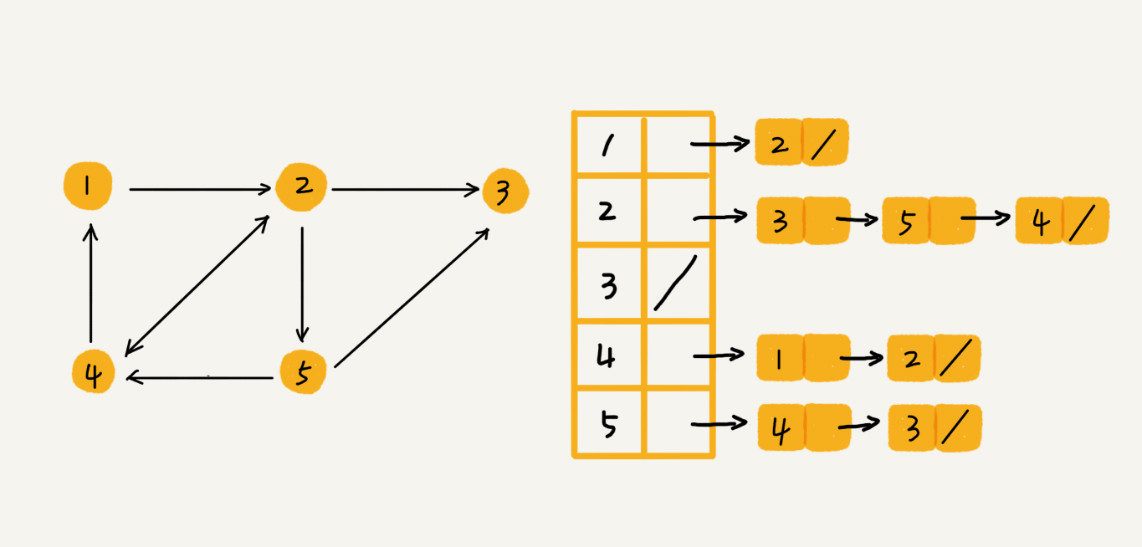
对于无向图来说,也是类似的,不过,每个顶点的链表中存储的,是跟这个顶点有边相连的顶点。
优缺点
邻接表存储起来比较节省空间,但是使用起来就比较耗时间。
搜索
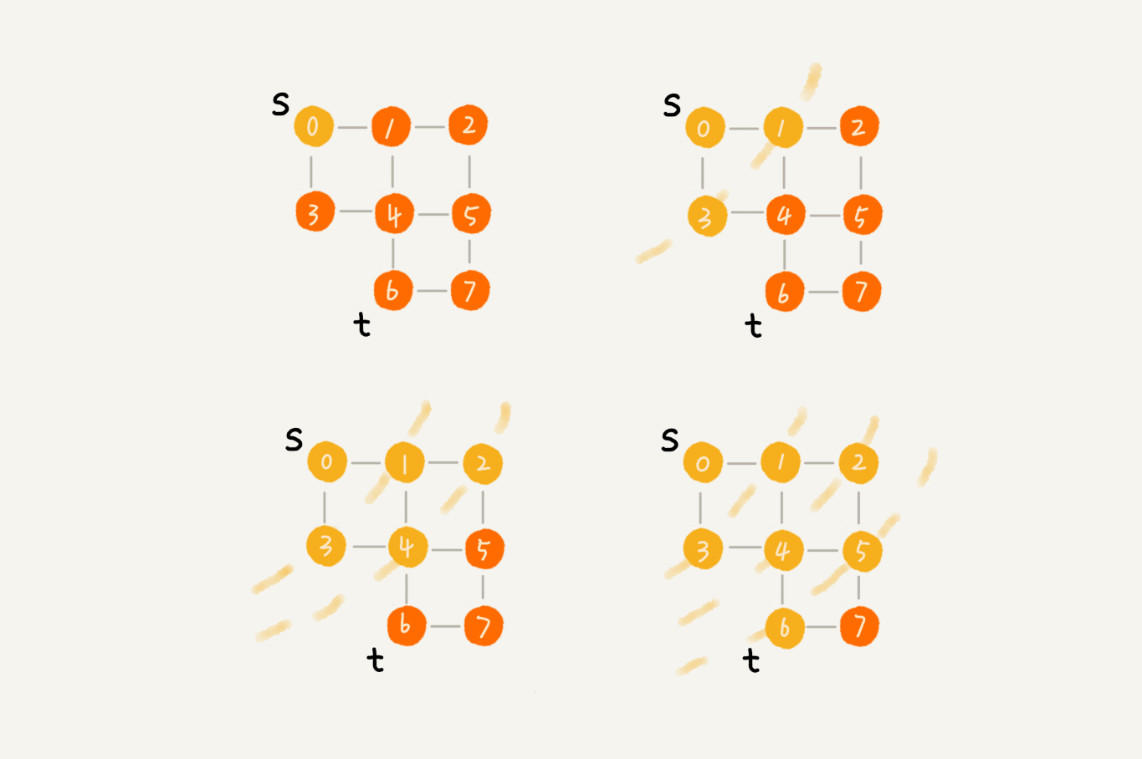
广度优先
直观地讲,它其实就是一种“地毯式”层层推进的搜索策略,即先查找离起始顶点最近的,然后是次近的,依次往外搜索。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
| public void bfs(int s, int t) {
if (s == t) {
return;
}
boolean[] visited = new boolean[v];
visited[s] = true;
Queue<Integer> queue = new LinkedList<>();
queue.add(s);
int[] prev = new int[v];
for (int i = 0; i < v; ++i) {
prev[i] = -1;
}
while (queue.size() != 0) {
int w = queue.poll();
for (int i = 0; i < adj[w].size(); ++i) {
int q = adj[w].get(i);
if (!visited[q]) {
prev[q] = w;
if (q == t) {
print(prev, s, t);
return;
}
visited[q] = true;
queue.add(q);
}
}
}
}
private void print(int[] prev, int s, int t) {
if (prev[t] != -1 && t != s) {
print(prev, s, prev[t]);
}
System.out.print(t + " ");
}
|
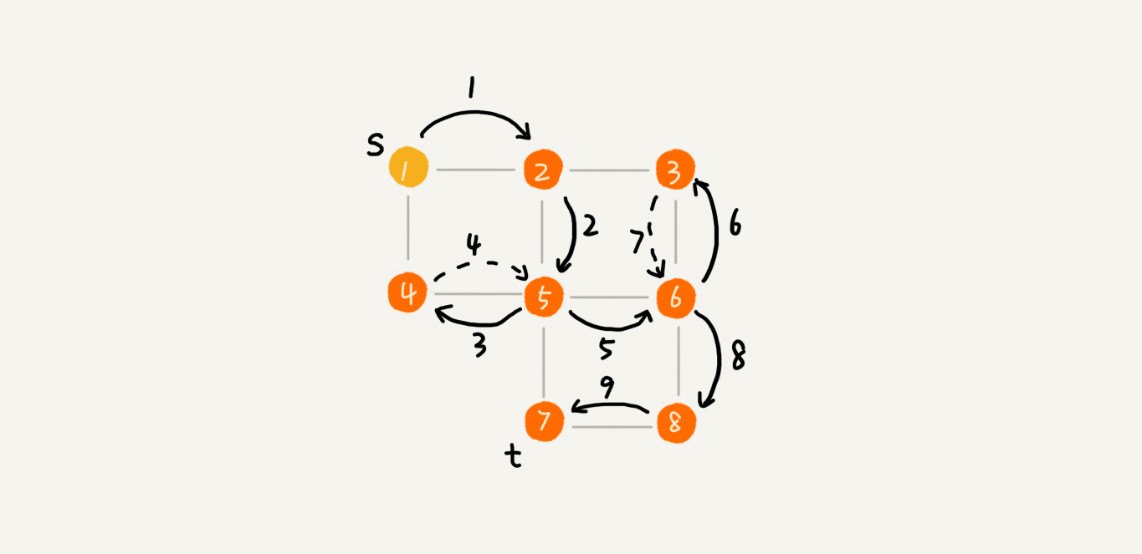
深度优先
最直观的例子就是“走迷宫”。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
|
private boolean found = false;
public void dfs(int s, int t) {
found = false;
boolean[] visited = new boolean[v];
int[] prev = new int[v];
for (int i = 0; i < v; ++i) {
prev[i] = -1;
}
recurDfs(s, t, visited, prev);
print(prev, s, t);
}
private void recurDfs(int w, int t, boolean[] visited, int[] prev) {
if (found) {
return;
}
visited[w] = true;
if (w == t) {
found = true;
return;
}
for (int i = 0; i < adj[w].size(); ++i) {
int q = adj[w].get(i);
if (!visited[q]) {
prev[q] = w;
recurDfs(q, t, visited, prev);
}
}
}
|





