排序--堆排序

特征

堆是一个完全二叉树
堆中每一个节点的值都必须大于等于（或小于等于）其子树中每个节点的值

之所以要求特征1，是因为完全二叉树要求除了最后一层，其他层的节点个数都是满的，最后一层的节点都靠左排列，这样用数组存储就不会有空隙。
对于每个节点的值都大于等于子树中每个节点值的堆，我们叫作“大顶堆”。对于每个节点的值都小于等于子树中每个节点值的堆，我们叫作“小顶堆”。

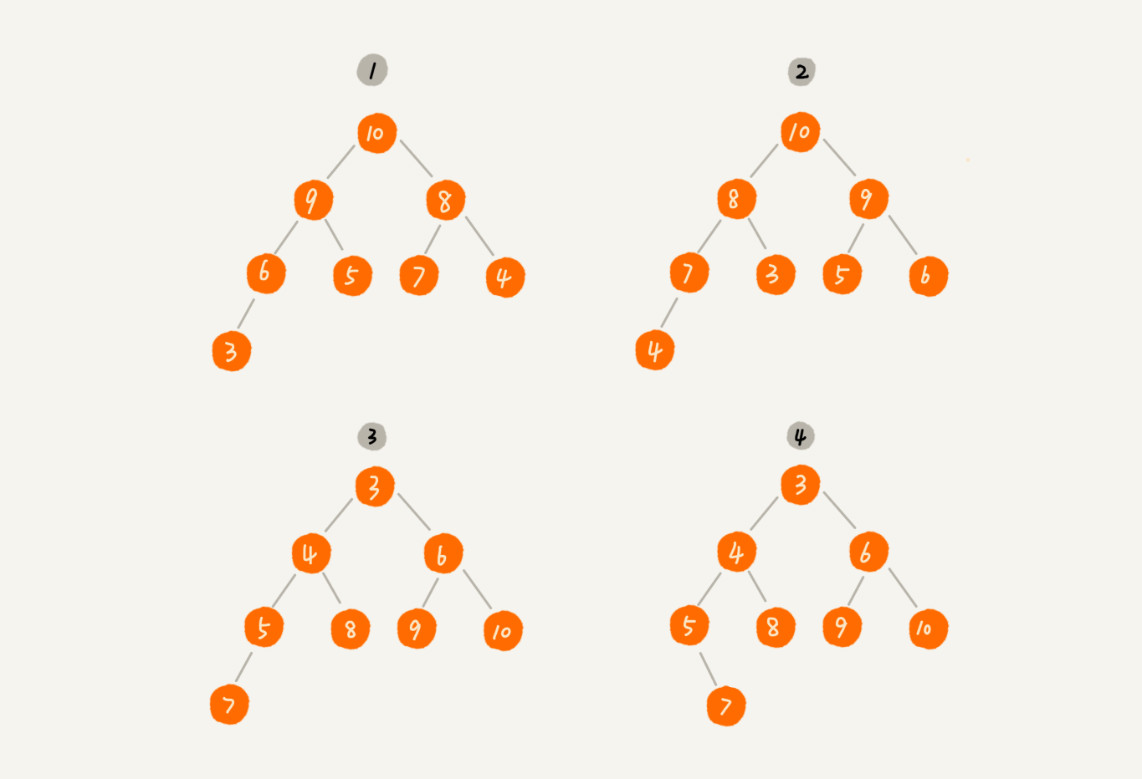
上图中，1、2是大顶堆，3是小顶堆，4不是顶堆。

存储

根据堆的特征1，堆适用用数组来存储。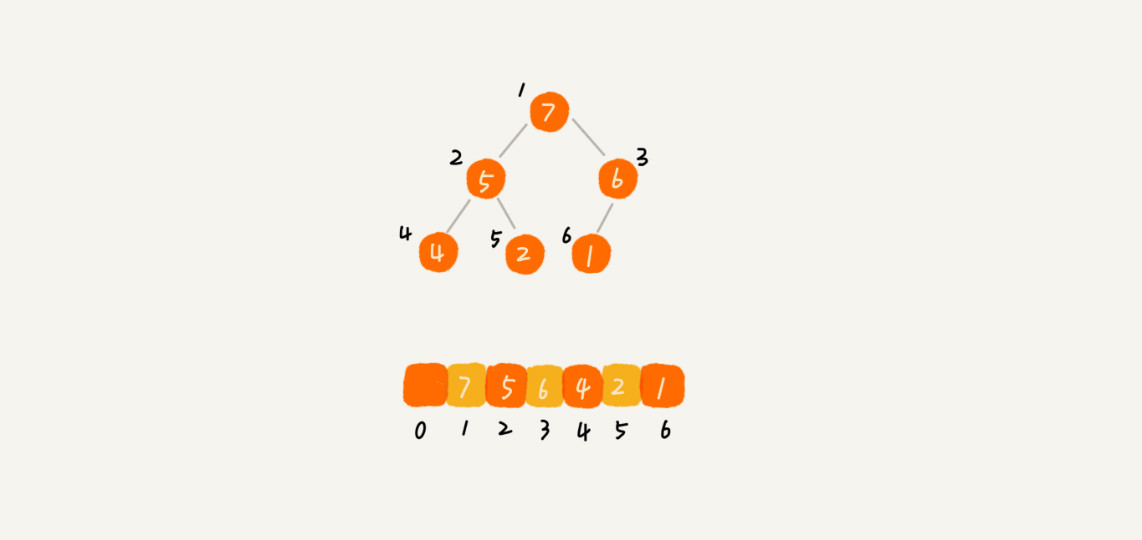

从图中我们可以看到，数组中下标为i的节点的左子节点，就是下标为i ∗ 2i的节点，右子节点就是下标为i ∗ 2 + 1的节点，父节点就是下标为i/2的节点。

堆化

从下往上

让新插入的节点与父节点对比大小。如果不满足子节点小于等于父节点的大小关系，我们就互换两个节点。一直重复这个过程，直到父子节点之间满足刚说的那种大小关系。

示例：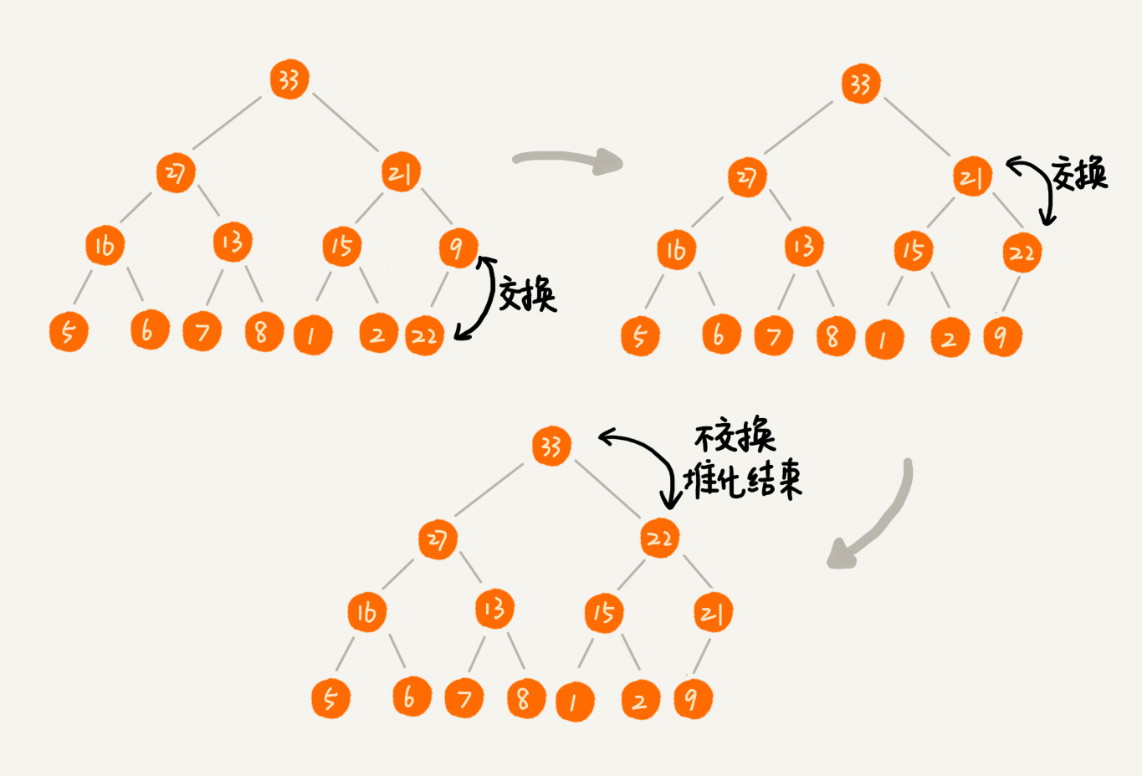

代码：

public class Heap {
    private int[] a; // 数组，从下标 1 开始存储数据
    private int n;  // 堆可以存储的最大数据个数
    private int count; // 堆中已经存储的数据个数
    
    public Heap(int capacity) {
        a = new int[capacity + 1];
        n = capacity;
        count = 0;
    }
    
    public void insert(int data) {
        if (count >= n) return; // 堆满了
        ++count;
        a[count] = data;
        int i = count;
        while (i / 2 > 0 && a[i] > a[i / 2]) { // 自下往上堆化
            swap(a, i, i / 2); // swap() 函数作用：交换下标为 i 和 i/2 的两个元素
            i = i / 2;
        }
    }
}

从上往下

把最后一个节点放到堆顶，然后利用同样的父子节点对比方法。对于不满足父子节点大小关系的，互换两个节点，并且重复进行这个过程，直到父子节点之间满足大小关系为止。这就是从上往下的堆化方法。

示例：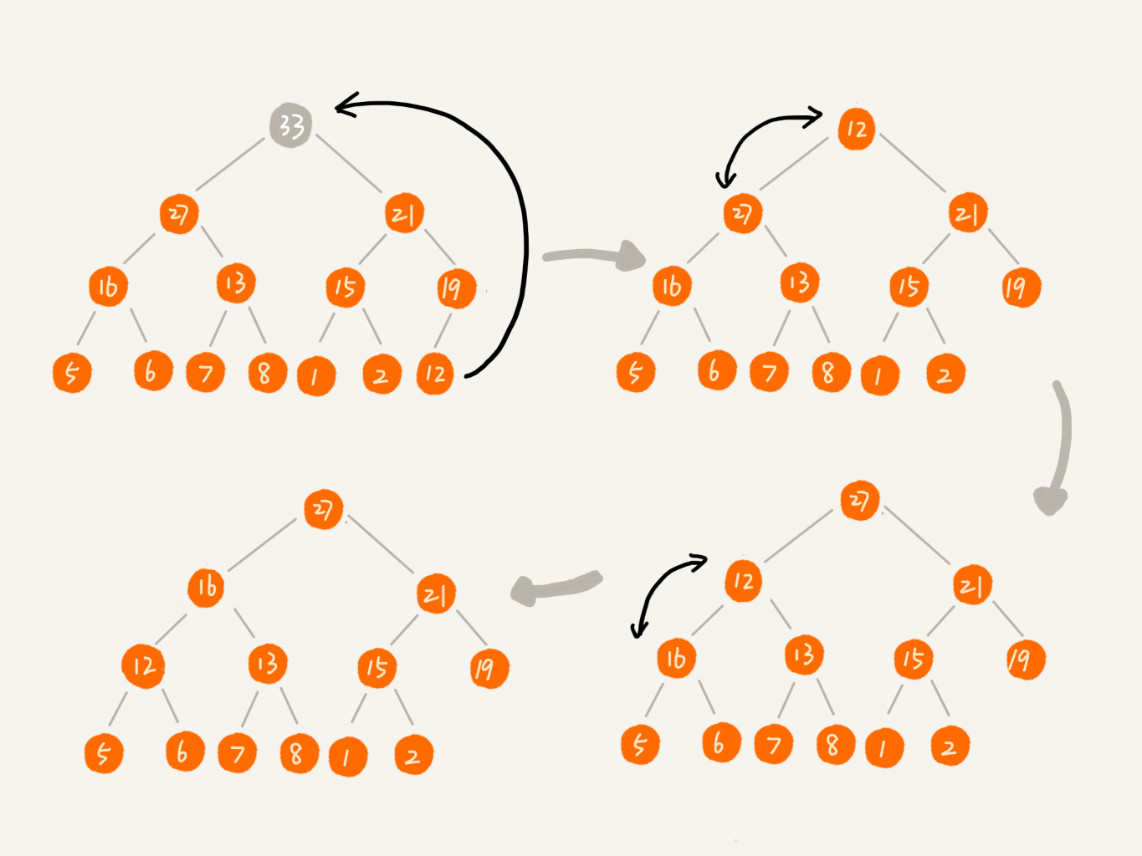

代码：

public void removeMax() {
    if (count == 0) return -1; // 堆中没有数据
    a[1] = a[count];
    --count;
    heapify(a, count, 1);
}

private void heapify(int[] a, int n, int i) { // 自上往下堆化
    while (true) {
        int maxPos = i;
        if (i*2 <= n && a[i] < a[i*2]) maxPos = i*2;
        if (i*2+1 <= n && a[maxPos] < a[i*2+1]) maxPos = i*2+1;
        if (maxPos == i) break;
        swap(a, i, maxPos);
        i = maxPos;
    }
}

时间复杂度

一个包含n个节点的完全二叉树，树的高度不会超过log2n。
堆化的过程是顺着节点所在路径比较交换的，所以堆化的时间复杂度跟树的高度成正比，也就是O(logn)。
插入数据和删除堆顶元素的主要逻辑就是堆化，所以，往堆中插入一个元素和删除堆顶元素的时间复杂度都是O(logn)。

堆排序

可以把堆排序的过程大致分解成两个大的步骤，建堆和排序。

建堆

有“从下往上堆化”和“从上往下堆化”两种方式，后者效率更高，因为它只需要依次堆化非叶子节点。建堆时间复杂度为O(n)。

从下往上堆化

将下表从1到n的数据依次插入到堆中。

从上往下堆化

因为叶子节点往下堆化只能自己跟自己比较，所以我们直接从第一个非叶子节点开始，依次堆化就行了。

示例：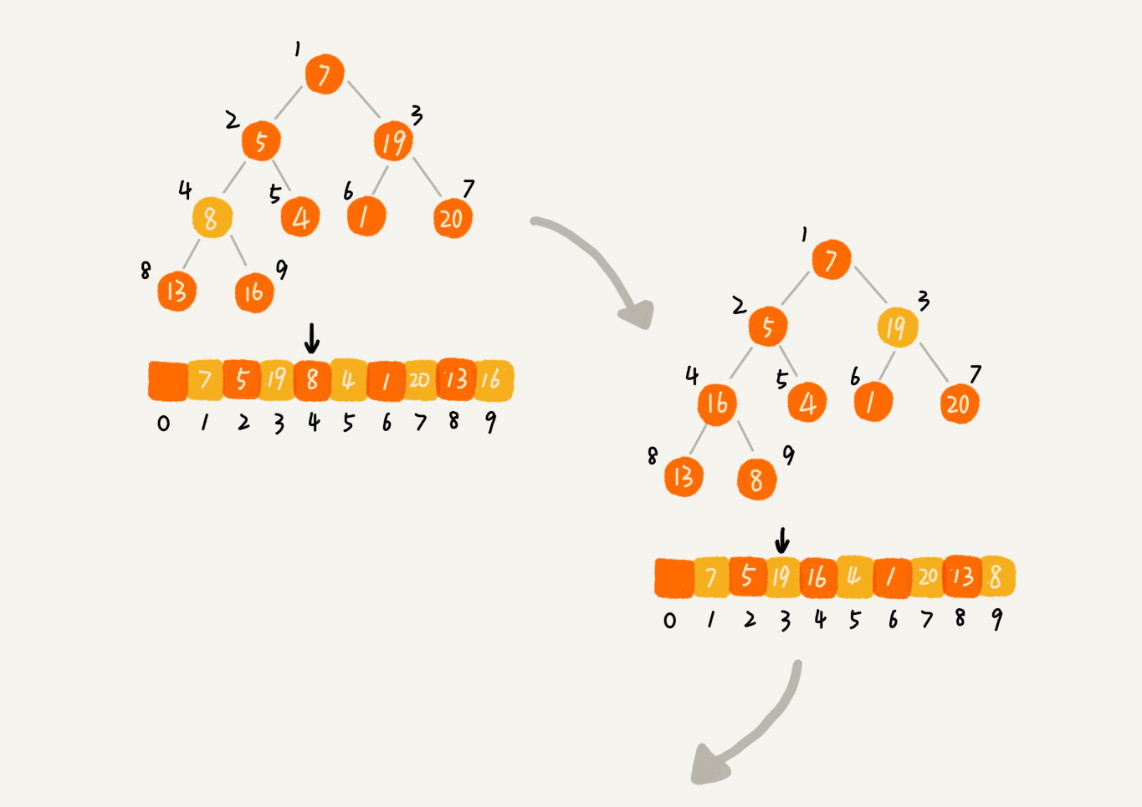

代码：

private static void buildHeap(int[] a, int n) {
    for (int i = n/2; i >= 1; --i) {
        heapify(a, n, i);
    }
}

private static void heapify(int[] a, int n, int i) {
    while (true) {
        int maxPos = i;
        if (i*2 <= n && a[i] < a[i*2]) maxPos = i*2;
        if (i*2+1 <= n && a[maxPos] < a[i*2+1]) maxPos = i*2+1;
        if (maxPos == i) break;
        swap(a, i, maxPos);
        i = maxPos;
    }
}

排序

建堆结束之后，数组中的数据已经是按照大顶堆的特性来组织的。
数组中的第一个元素就是堆顶，也就是最大的元素。我们把它跟最后一个元素交换，那最大元素就放到了下标为n的位置。

这个过程有点类似上面讲的“删除堆顶元素”的操作，当堆顶元素移除之后，我们把下标为n的元素放到堆顶，然后再通过堆化的方法，将剩下的n−1个元素重新构建成堆。
堆化完成之后，我们再取堆顶的元素，放到下标是n−1的位置，一直重复这个过程，直到最后堆中只剩下标为 111 的一个元素，排序工作就完成了。

示例：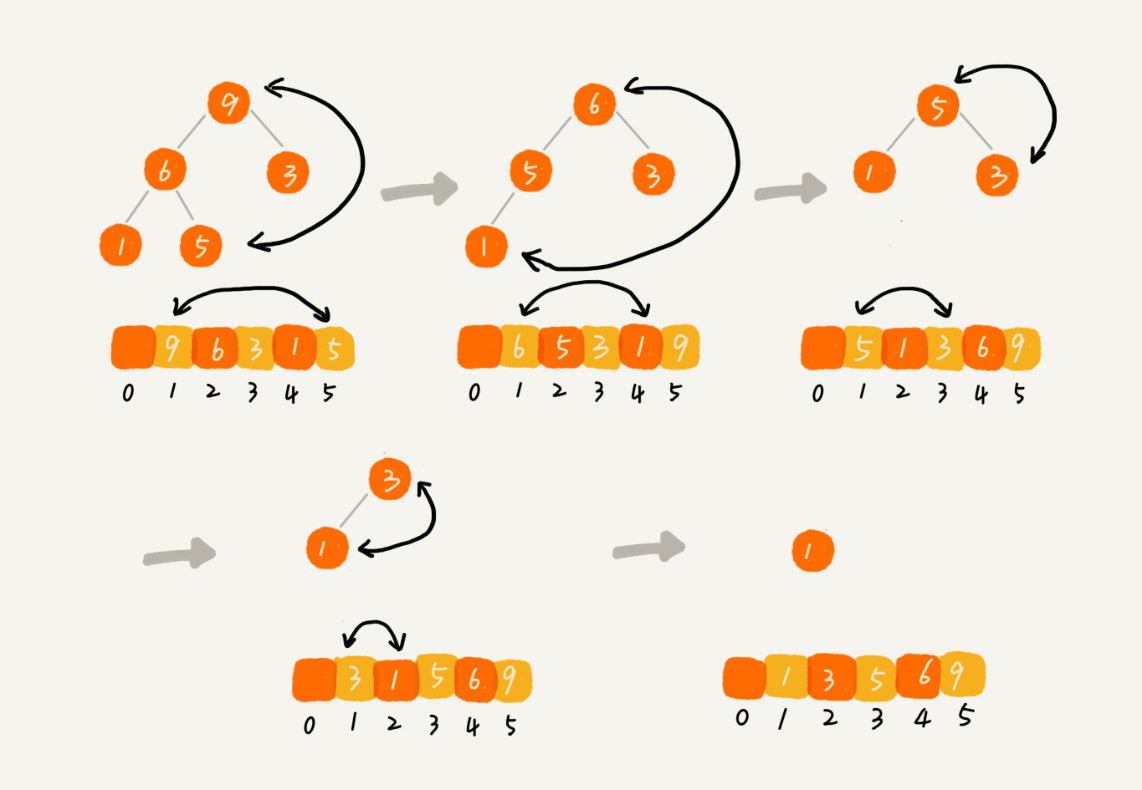

代码：

// n 表示数据的个数，数组 a 中的数据从下标 1 到 n 的位置。
public static void sort(int[] a, int n) {
  buildHeap(a, n);
  int k = n;
  while (k > 1) {
    swap(a, 1, k);
    --k;
    heapify(a, k, 1);
  }
}

时间复杂度：O(nlogn)

应用

优先级队列
- 合并有序小文件
- 高性能定时器
TOP K
中位数