由来
B+树通常用于实现索引,像Mysql索引就是基于B+树实现的,而索引除了要支持增删改查之外,还需要支持范围查询。并且由于索引通常是存在与磁盘上,这就还要求磁盘访问次数不能过多。
常用数据结构比较
- 散列表
查询时间复杂度O(1),不支持区间查询 - 红黑树
查询时间复杂度O(lon2n),对其进行中序遍历,能得到从小到大有序的数据序列,但不足以支持区间查询 - 跳表
查询时间复杂度O(lon2n),支持区间查询 - B+树
查询时间复杂度O(lon2n),支持区间查询
二叉树改造
我们可以对二叉查找树进行改造,从而让其支持区间查询:树中的节点并不存储数据本身,而是只是作为索引。除此之外,我们把每个叶子节点串在一条链表上,链表中的数据是从小到大有序的。经过改造之后的二叉树,就像图中这样: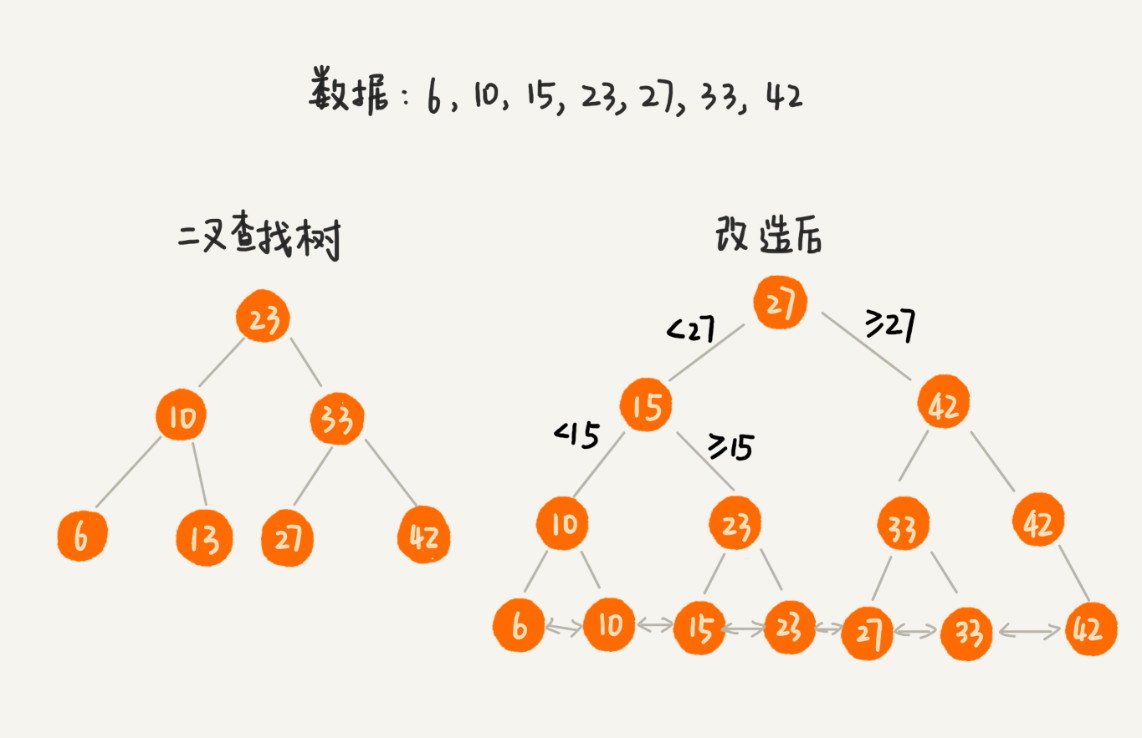
但是,当索引数据量达到几千万甚至上亿的时候,如果将索引存储在内存中,尽管内存访问的速度非常快,查询的效率非常高,但是占用的内存会非常多。
我们可以借助时间换空间的思路,把索引存储在硬盘中。不过磁盘是一个非常慢速的存储设备。通常内存的访问速度是纳秒级别的,而磁盘访问的速度是毫秒级别的。读取同样大小的数据,从磁盘中读取花费的时间,是从内存中读取所花费时间的上万倍,甚至几十万倍。这种将索引存储在硬盘中的方案,尽管减少了内存消耗,但是在数据查找的过程中,需要读取磁盘中的索引,因此数据查询效率就相应降低很多。
那么,接下来优化的重点就是尽量减少磁盘IO操作,也就是尽量降低树的高度:实现m叉树。
特征
- 每个节点中子节点的个数不能超过 m,也不能小于 m/2
- 根节点的子节点个数可以不超过 m/2,这是一个例外
- m叉树只存储索引,并不真正存储数据,这个有点儿类似跳表
- 通过链表将叶子节点串联在一起,这样可以方便按区间查找
- 一般情况,根节点会被存储在内存中,其他节点存储在磁盘中
分裂&合并
分裂
不管是内存中的数据,还是磁盘中的数据,操作系统都是按页来读取的,一次会读一页的数据。如果要读取的数据量超过一页的大小,就会触发多次IO操作。所以,我们在选择m大小的时候,要尽量让每个节点的大小等于一个页的大小。读取一个节点,,只需要一次磁盘IO操作。
对于一个B+树来说,m值是根据页的大小事先计算好的,也就是说,每个节点最多只能有m个子节点。在往数据库中写入数据的过程中,这样就有可能使索引中某些节点的子节点个数超过m,这个节点的大小超过了一个页的大小,读取这样一个节点,就会导致多次磁盘IO操作。
我们只需要将这个节点分裂成两个节点。但是,节点分裂之后,其上层父节点的子节点个数就有可能超过 m 个。不过这也没关系,我们可以用同样的方法,将父节点也分裂成两个节点。这种级联反应会从下往上,一直影响到根节点。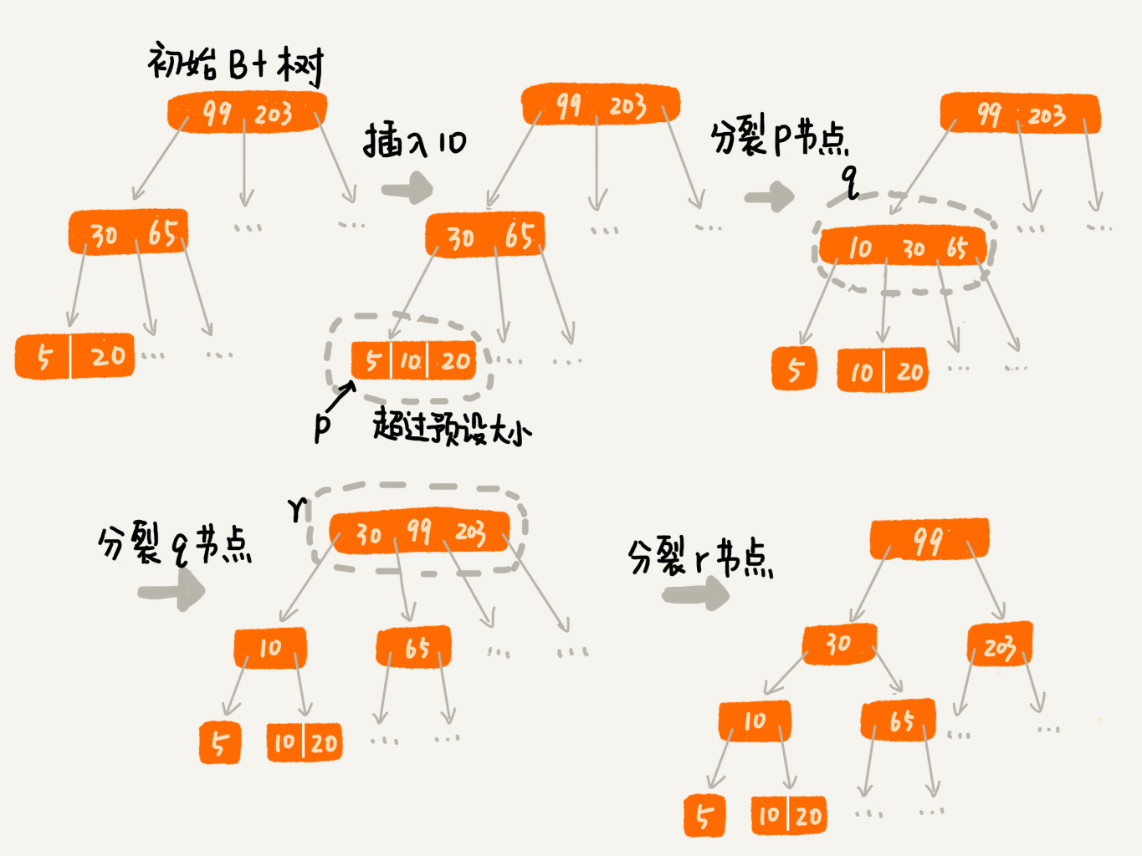
合并
频繁的数据删除,就会导致某些结点中,子节点的个数变得非常少,长此以往,如果每个节点的子节点都比较少,势必会影响索引的效率。
我们可以设置一个阈值。在B+树中,这个阈值等于m/2。如果某个节点的子节点个数小于m/2,我们就将它跟相邻的兄弟节点合并。不过,合并之后结点的子节点个数有可能会超过m。针对这种情况,我们可以借助插入数据时候的处理方法,再分裂节点。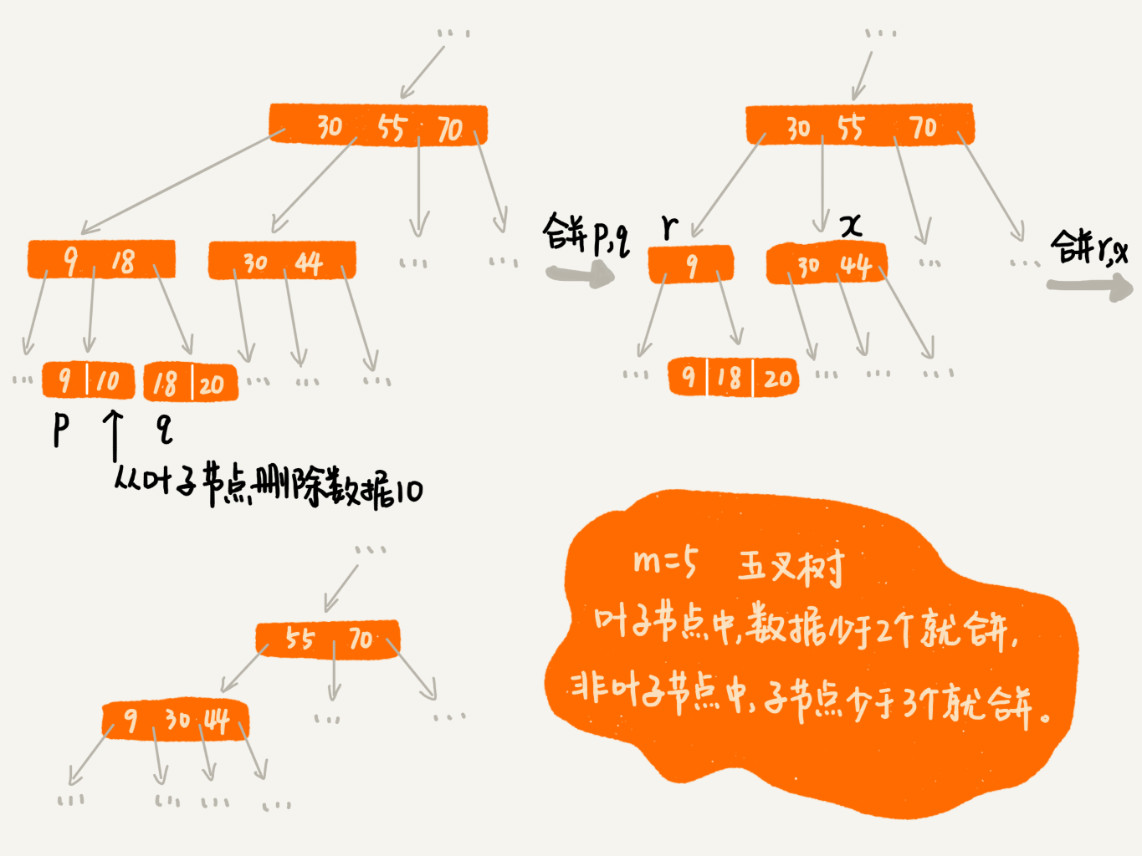
b*树
B* 树是B+树的变体,在B+树的非根和非叶子结点再增加指向兄弟的指针;B树定义了非叶子结点关键字个数至少为(2/3)M,即块的最低使用率为2/3(代替B+树的1/2)。
- B+树的分裂
当一个结点满时,分配一个新的结点,并将原结点中1/2的数据复制到新结点,最后在父结点中增加新结点的指针;B+树的分裂只影响原结点和父结点,而不会影响兄弟结点,所以它不需要指向兄弟的指针 - B* 树的分裂
当一个结点满时,如果它的下一个兄弟结点未满,那么将一部分数据移到兄弟结点中,再在原结点插入关键字,最后修改父结点中兄弟结点的关键字(因为兄弟结点的关键字范围改变了);如果兄弟也满了,则在原结点与兄弟结点之间增加新结点,并各复制1/3的数据到新结点,最后在父结点增加新结点的指针
所以,B* 树分配新结点的概率比B+树要低,空间使用率更高;

