类别
- 二叉树
每个节点最多有两个“叉”,也就是两个子节点,分别是左子节点和右节点。
- 满二叉树
除了叶子节点之外,每个节点都有左右两个子节点。
- 完全二叉树
若设二叉树的深度为h,除第h层外,其它各层(1~h-1)的结点数都达到最大个数,第h层所有的结点都连续集中在最左边。
- 平衡二叉树
左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
存储
链式存储法
每个节点有三个字段,其中一个存储数据,另外两个是指向左右子节点的指针。我们只要拎住根节点,就可以通过左右子节点的指针,把整棵树都串起来。
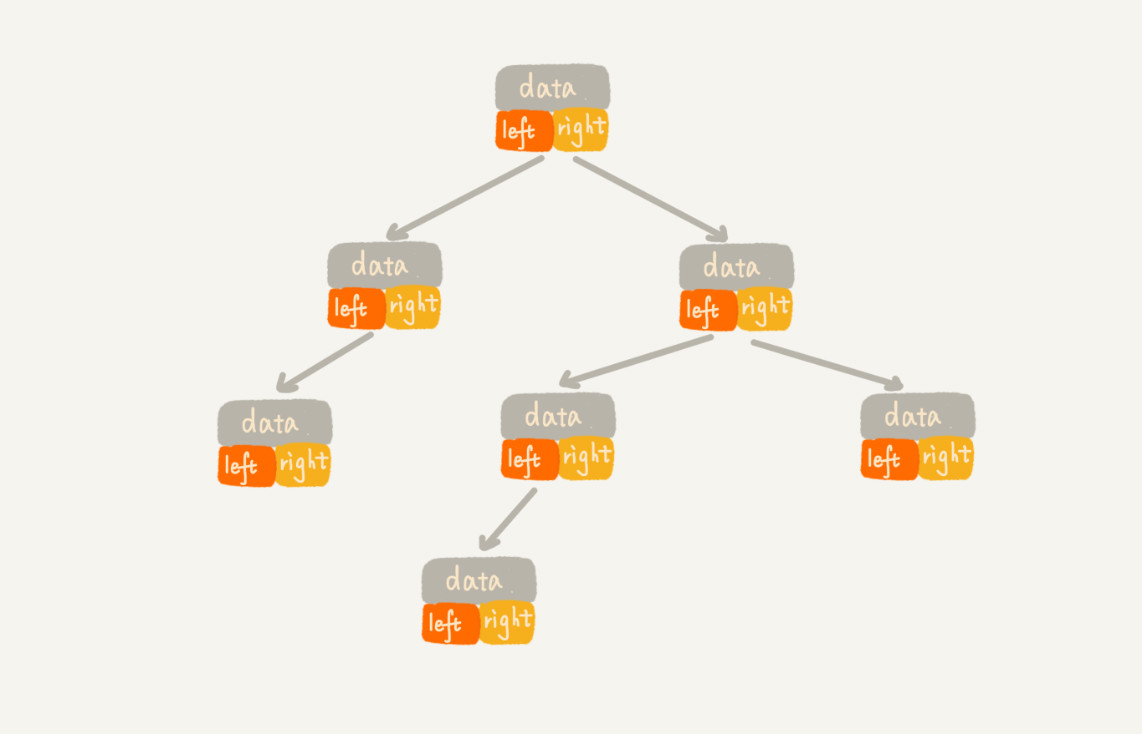
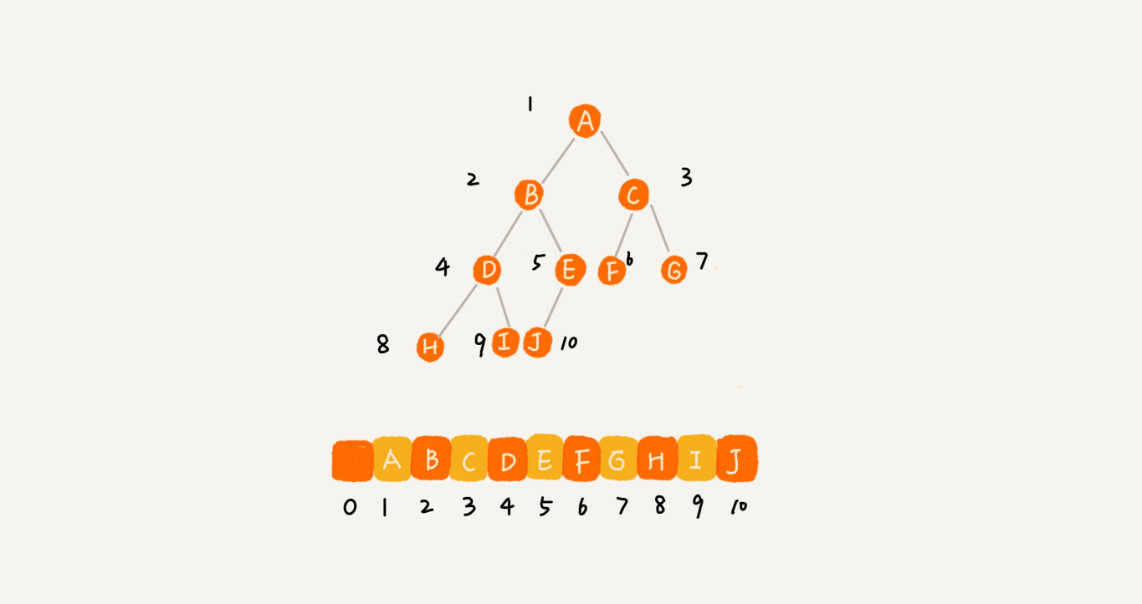
顺序存储法
把根节点存储在下标i = 1的位置,那左子节点存储在下标2 * i = 2的位置,右子节点存储在2 * i + 1 = 3的位置。以此类推。
遍历
前序遍历
对于树中的任意节点来说,先打印这个节点,然后再打印它的左子树,最后打印它的右子树。
1
2
3
4
5
6
7
8
9
| ```java
public void preOrder(BinaryTree root) {
if (root == null) {
return;
}
System.out.println(root.data);
preOrder(root.left);
preOrder((root.right));
}
|
中序遍历
对于树中的任意节点来说,先打印它的左子树,然后再打印这个节点,最后打印它的右子树。
1
2
3
4
5
6
7
8
9
| ```java
public void inOrder(BinaryTree root) {
if (root == null) {
return;
}
preOrder(root.left);
System.out.println(root.data);
preOrder((root.right));
}
|
后序遍历
对于树中的任意节点来说,先打印它的右子树,然后再打印它的左子树,最后打印这个节点。
1
2
3
4
5
6
7
8
9
| ```java
public void postOrder(BinaryTree root) {
if (root == null) {
return;
}
preOrder(root.left);
preOrder((root.right));
System.out.println(root.data);
}
|
层序遍历
按层遍历。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
| public List<List<Integer>> levelOrder(TreeNode root) {
if (root == null) return new ArrayList<>(0);
List<List<Integer>> result = new ArrayList<>();
Queue<TreeNode> queue = new LinkedList<TreeNode>();
queue.offer(root);
Queue<TreeNode> curLevelNodes = new LinkedList<TreeNode>();
while (!queue.isEmpty()) {
TreeNode node = queue.poll();
curLevelNodes.offer(node);
if (queue.isEmpty()) {
List<Integer> list = new ArrayList<>(curLevelNodes.size());
while (!curLevelNodes.isEmpty()) {
TreeNode curNode = curLevelNodes.poll();
list.add(curNode.val);
if (curNode.left != null) {
queue.offer(curNode.left);
}
if (curNode.right != null) {
queue.offer(curNode.right);
}
}
result.add(list);
}
}
return result;
}
|
基本操作
查找
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| public BinaryTree find(BinaryTree tree, int data) {
BinaryTree root = tree;
while (root != null) {
if (tree.data == data) {
return tree;
} else if (tree.data < data) {
root = root.right;
} else {
root = root.left;
}
}
return null;
}
|
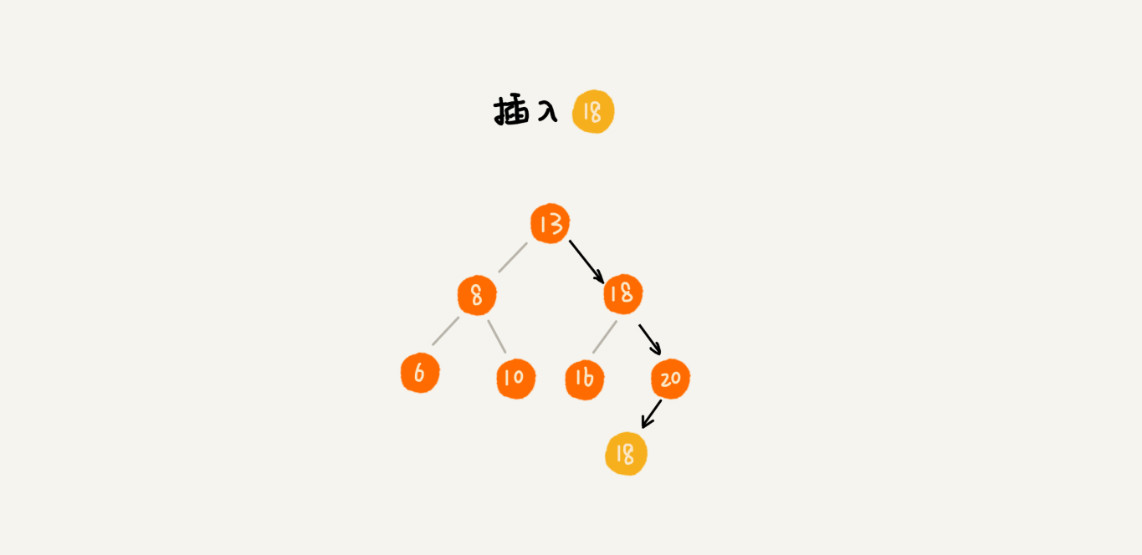
插入
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| public void insert(BinaryTree tree, int data) {
if (tree == null) {
tree = new BinaryTree(data);
return;
}
BinaryTree root = tree;
while (true) {
if (data > tree.data) {
if (root.right == null) {
root.right = new BinaryTree(data);
return;
}
root = root.right;
} else if (data < tree.data) {
if (root.left == null) {
root.left = new BinaryTree(data);
return;
}
root = root.left;
}
}
}
|
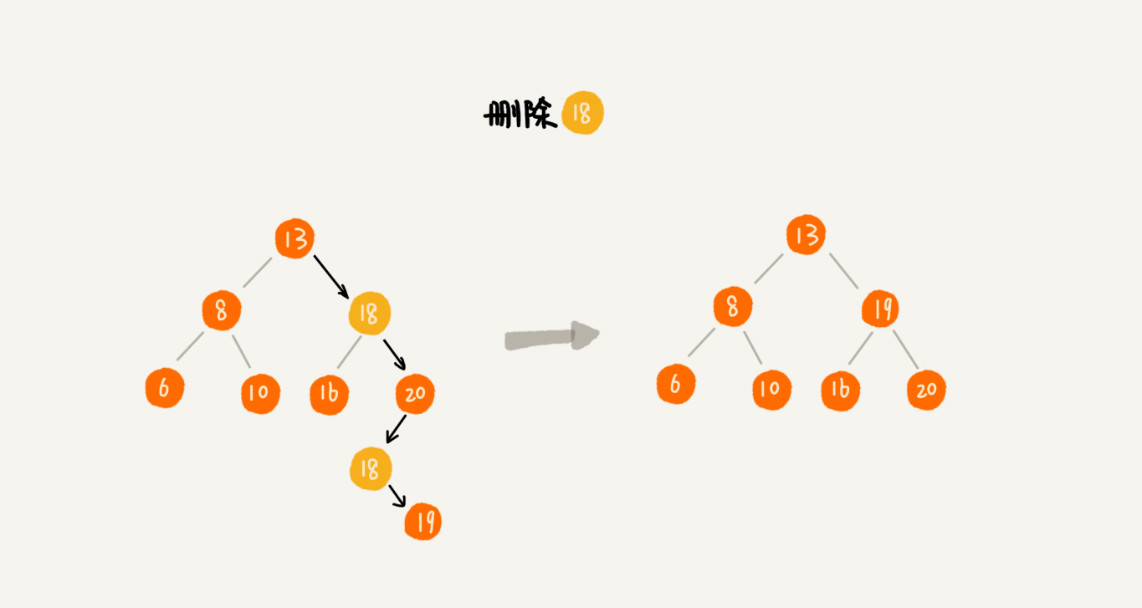
删除
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
| public void delete(BinaryTree tree, int data) {
BinaryTree p = tree;
BinaryTree pp = null;
while (p != null && p.data != data) {
pp = p;
if (p.data > data) {
p = p.left;
} else {
p = p.right;
}
}
if (p == null) {
return;
}
if (p.left != null && p.right != null) {
BinaryTree minp = p.right;
BinaryTree minpp = p;
while (minp.left != null) {
minpp = minp;
minp = minp.left;
}
p.data = minp.data;
p = minp;
pp = minpp;
}
BinaryTree child;
if (p.left != null) {
child = p.left;
} else if (p.right != null) {
child = p.right;
} else {
child = null;
}
if (pp == null) {
tree = child;
}
else if (pp.left == p) {
pp.left = child;
}
else {
pp.right = child;
}
}
|
重复数据
在前面的操作中,都是假定不存在键值相同的情况。如果存在重复数据,有两种解决方式。
方式一
一种是二叉查找树中每一个节点不仅会存储一个数据,因此我们通过链表和支持动态扩容的数组等数据结构,把值相同的数据都存储在同一个节点上。
方式二
另一种是每个节点仍然只存储一个数据。
在查找插入位置的过程中,如果碰到到一个节点的值,与要插入数据的值相同,我们就将这个要插入的数据放到这个节点的右子树,也就是说,把这个新插入的数据当作大于这个节点的值来处理。
当要查找数据的时候,遇到值相同的节点,我们并不停止查找操作,而是继续在右子树中查找,直到遇到叶子节点,才停止。这样就可以把键值等于要查找值的所有节点都找出来。
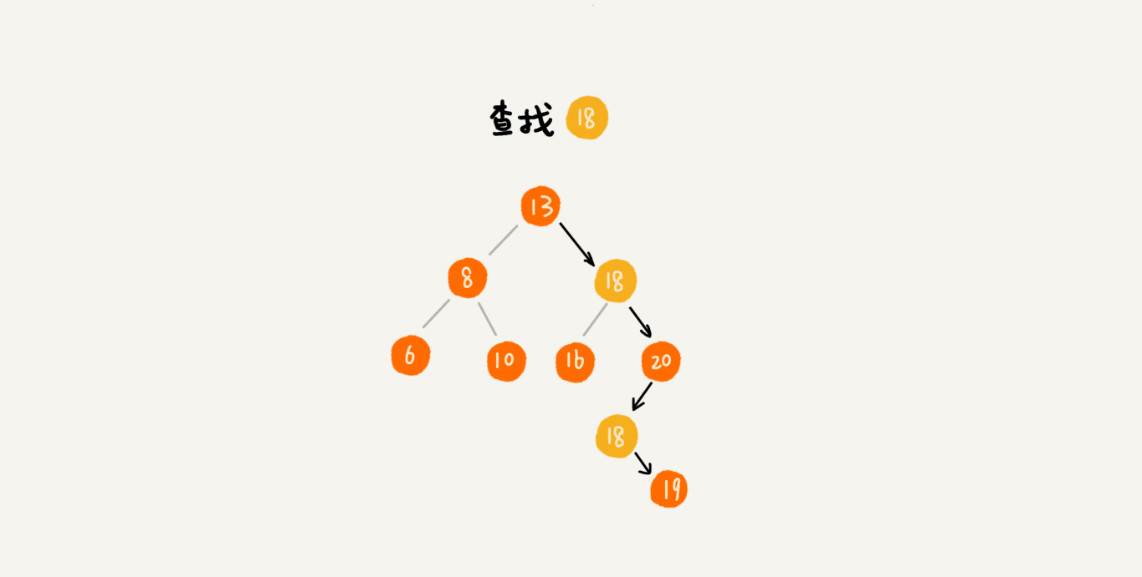
对于删除操作,我们也需要先查找到每个要删除的节点,然后再按前面讲的删除操作的方法,依次删除。