红黑树是一种自平衡二叉树:即在频繁的动态更新过程中,不会出现树的高度远大于log2n的情况,从而导致各个操作的效率下降。
红黑树具有以下性质:
- 节点是红色或黑色
- 根节点是黑色
- 任何相邻的节点都不能同时为红节点,也就是说,红节点是被黑节点隔开的
- 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点
- 每个叶子节点都是黑色的空节点(NIL),也就是说,叶子节点不存储数据
根据性质3可知,最短的可能路径都是黑节点,最长的可能路径都是交替的黑节点和红节点,而性质4要求所有路径都包含相同数目的黑色节点,这就约束强制了红黑树的关键性质:从根节点到叶子节点的最长的可能路径不多于最短的可能路径的两倍长,即树的高度不会大于2lon2n。
我们知道,魔方的复原解法是由固定的算法的:遇到哪几面是什么样子,就对应怎么转几下。红黑树的自平衡过程跟魔方的复原非常神似,大致过程就是:遇到什么样的节点排布,就对应怎么去调整。只要按照这些固定的调整规则来操作,就能将一个非平衡的红黑树调整成平衡的。
上面的性质5:每个叶子节点都是黑色的空节点(NIL),就是为了方便的实现自平衡而添加的约束。
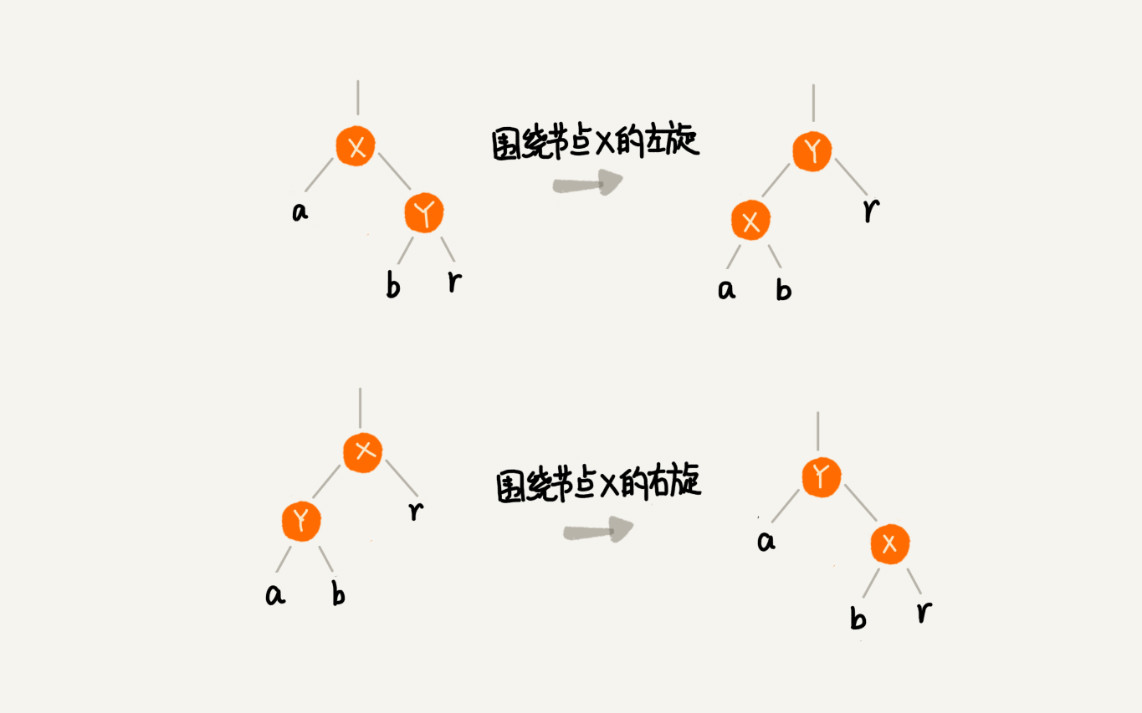
至于红黑树具体是怎样进行自平衡操作的,则首先需要了解两个非常重要的操作:左旋(rotate left)、右旋(rotate righ)。示例: